Quick Crosswind Calculation for Pilots

As soon as you start flying, you’ll quickly learn that the wind nearly always has a sideways component. But how strong is it, and how big will its effects be? Relax. There is a quick, easy and reliable way to work it out. Today we demonstrate how to perform a quick crosswind calculation and why it is important to know.

How to Do a Quick Crosswind Calculation

The quickest method to calculate the crosswind is the ‘clock face method’. This will provide an approximate answer as to the crosswind component. It is easy to achieve if you can tell the time and have a very basic understanding of math. Even professional pilots use this technique!

 To calculate the crosswind, you will need three key pieces of information: –

• The aircraft heading
• The wind direction
• The wind speed

Yes, that is literally it!

Using a little simple math and a fair handful of ’rounding’, you can make a really good estimate as to what the crosswind is.

Keep reading to find out how to do it.

What is a Crosswind?

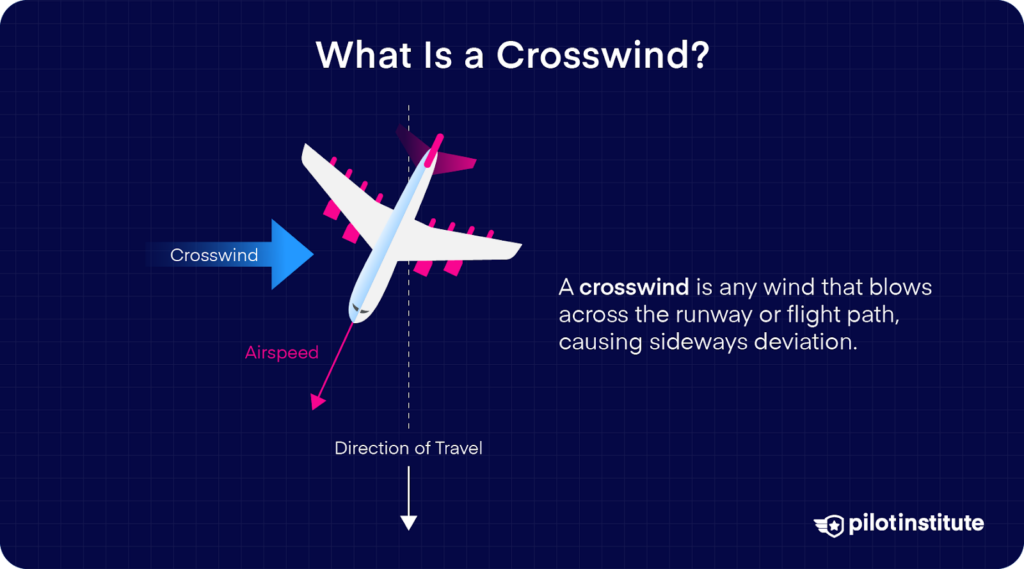
Before we begin, let’s go back to basics.

Just what is a crosswind?

As the name would suggest, a crosswind is any wind element that imparts sideways deviation on the aircraft… I.e., across.

And we’ve got news for you.

There will always be a crosswind component unless the wind is coming from directly in front of you or behind you.

Two things determine how great the crosswind component is.

Namely…

The direction the wind is coming from relative to your aircraft and its strength.

A relatively mild wind coming from 90° on either side of the aircraft has far less effect than a strong wind coming from the same direction.

Furthermore…

If the wind is strong, even small differences between its angle and the aircraft’s heading can have a significant effect.

Crosswind is referenced in terms of ‘knots’, a fancy aviation term for ‘nautical miles per hour.

Before we go into detail about performing a quick crosswind calculation, here is how the ‘math’ behind it works in detail.

Trigonometry and Crosswind Calculations

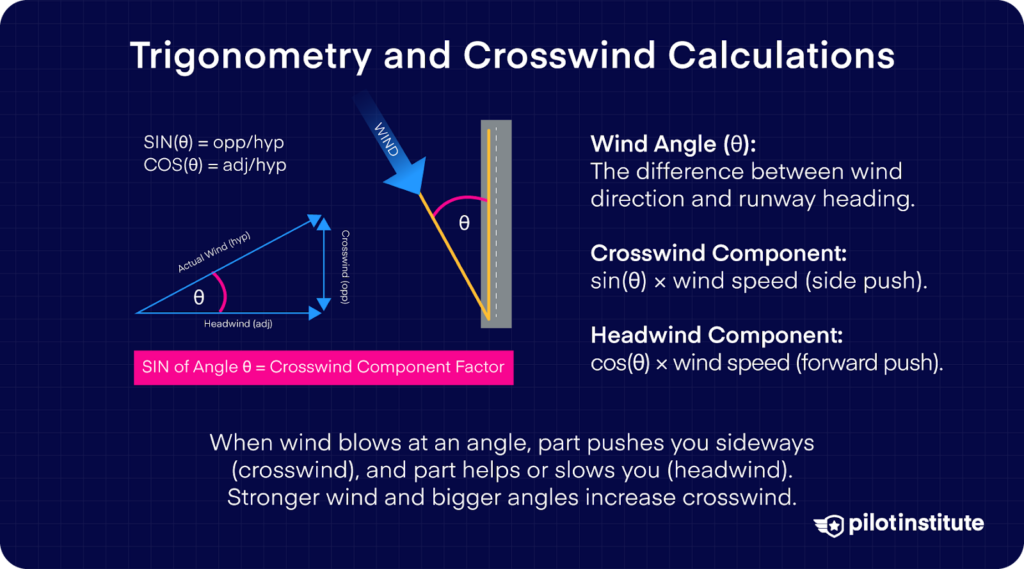
Familiar with trigonometry?

If not, don’t worry too much as we will explain it in really simple terms. By the end of this article, it will all make sense.

Trigonometry is the study of angles and how they interact in various geometric shapes.

Don’t panic…

By having a basic understanding of trigonometry, we can apply a few simple rules that make a quick crosswind calculation really easy.

What rules?

Well, remember the following, and you’ll be in a great place: –

• “The greatest effect from crosswind will be observed when the wind is 90° from your heading.”
• “The smallest effect of crosswind will be observed when the difference between the wind and your heading is 0°.”

See? That wasn’t too hard, was it?

By learning these two simple rules, we already have a great handle on how trigonometry plays a part in a quick crosswind calculation.

Why?

Reading between the lines… If 90° winds cause the greatest crosswind effect and 0° wind has the least effect, we can safely assume there is some linear gradient when the wind falls between these two angles.

This linear gradient has a name in trigonometry.

It is called sine.

Neat, right?

Sine is the name given to a trigonometric function. It is at its highest when an angle reaches 90° and at its lowest when the angle is 0°. Fortunately for us, as aviators, the value of sine can also be calculated for every angle in between too!

How does this help with crosswind calculations?

Considering the above rules, we need to multiply the wind speed by sine to give us a crosswind component strength.

Want a working example?

Check out the table below showing sine for a range of angles. Once you’ve checked the table, see how it applies to our examples below.

Pay particular attention to the highlighted angles and their sine… They will be important a little later when we show you how to perform a really quick crosswind calculation…

Angle	Sine of the Angle
10	0.17
15	0.25
20	0.34
25	0.42
30	0.5
35	0.57
40	0.64
45	0.70
50	0.75
55	0.81
60	0.86
65	0.90
70	0.94
75	0.96
80	0.98
85	0.99
90	1

Here’s how the above works concerning crosswind.

Remember, we need to multiply the angular difference between the wind and our heading to work out the crosswind component.

Example 1)

• Aircraft heading: 070°
• Wind Direction:160°
• Wind Strength: 25 knots

This example is super easy.

The angular difference between the aircraft heading and wind direction is exactly 90°. The sine of 90° is 1. The wind strength is 25 knots.

So…

1 (the sine of 90°) X 25 (knots) = A crosswind component of 25 knots.

Simple, right?

Well, watch what happens in our next example…

Example 2)

• Aircraft heading: 070°
• Wind Direction:100°
• Wind Strength: 50 knots

The wind has now shifted and is only 30° different from our heading. Now, you may think that the crosswind component will be lower…

Let’s see what happens when we do the math.

So, the sine of 30° is 0.5. And the wind strength is 50 knots.

0.5 x 50 = 25 knots of crosswind!

But, wait…

We know what you are thinking.

How is the crosswind component still the same when the angle is less?

Pay attention to the wind strength. Sure, the angle is less, but the overall strength of the wind is higher. Meaning both of the above examples have exactly the same crosswind component.

Here’s a compact table where the wind speed stays the same and only the direction changes to make life easy. All of the results calculated in this table were arrived at using the formula you’ve seen in the examples above: –

 We’d get the following crosswind components with a wind strength of 40 knots.

Angular Difference Between Heading and Wind	Sine of the Angle	Resulting Crosswind
0	0
10	0.17	6.8 knots
20	0.34	13.6 knots
30	0.5	20 knots
40	0.64	25.6 knots
50	0.76	30.4 knots
60	0.86	34.4 knots
70	0.93	37.2 knots
80	0.98	39.2 knots
90	1.0	40 knots

The takeaway from the above should be that the greater the angle, the stronger the crosswind! This simple concept is super useful to know when flying.

Now, granted, nobody recommends that you spend valuable flying time memorizing sine tables and working out angular differences.

Thankfully, there is an easier way to calculate crosswind.

Here’s a step-by-step guide to performing a quick crosswind calculation in seconds.

Quick Crosswind Calculation – A Step-by-Step Guide to the ‘Clock’ Method

Remember above when we told you to pay attention to the highlighted angles. The astute among you may have noticed something significant.

Don’t worry if you didn’t spot it.

It goes something like this.

The sine of the following angles allows us to perform a really quick crosswind calculation: –

• 15°
• 30°
• 45°
• 60°

Check the table again. Do you notice anything significant now?

Allow us to spell it out.

• 15° corresponds to 0.25 (or quarter) of the wind speed
• 30° corresponds to 0.5 (or half) of the wind speed
• 45° corresponds to just under 0.75 (or three quarters) of the wind speed
• 60° corresponds to 0.86 (which is nearly all) of the wind speed.

Can you think of anything else where 15 equals a quarter, 30 equals half, 45 equals three quarters, and 60 is ‘full’.

Want a hint? You wear it on your wrist to tell the time (OK, maybe that was a bit obvious).

You can perform a quick crosswind calculation if you can understand how many minutes there are in each hour.

Here’s how it is done: –

Step by Step Quick Crosswind Calculation

1. Make a note of the wind speed and general direction
2. Make a note of your heading and calculate the difference between this and the wind direction
3. Round the difference in wind direction and head up to the nearest 15 degrees (to a maximum of 60). So either 15°, 30°, 45°, or 60°.
4. Imagine the difference in terms of minutes on a clock face.
5. Apply the following rules: –
   • If the wind is 15° off, then the crosswind component is a quarter of the full strength of the wind (15 minutes is a quarter of an hour)
   • If the wind is 30° off, then the crosswind component is half of the full strength of the wind (30 minutes is half an hour)
   • If the wind is 45° off, then the crosswind component is three-quarters of the full strength of the wind (45 minutes is three-quarters of an hour).
   • If the wind is 60° off, then the crosswind component is nearly the full strength of the wind (60 minutes is a full hour).

Let’s see the above in action. We’ll use a 20-knot wind.

• At 15° difference, the crosswind would be approximately 5 knots
• At 30° difference, the crosswind would be approximately 10 knots
• At 45° difference, the crosswind would be approximately 15 knots
• At 60° or greater difference, the crosswind would be approximately 20 knots

Check the results against the above sine table if you doubt how accurate this is. There might be the occasional difference of a knot or two here or there, but, generally, as we pilots say, “it is close enough for government work”.

Try the above method with winds of different strengths. You’ll find that it works really well to quickly calculate crosswind.

5 Reasons to Perform a Quick Crosswind Calculation

Now that you have mastered an easy technique to quickly calculate crosswind, you may be wondering why it is so important to know this information. Well, there are plenty of good reasons.

Such as…

Navigation

An old, bold pilot once told us that a weather forecast is simply ‘a horoscope with numbers’.

And do you know what?

They were right.

Even with the best weather data in the world, things can change quickly. If you get aloft and realize your navigation isn’t working out, it could be the wind.

You won’t have time to be messing around with a flight computer or crosswind chart. The time has come for a ‘quick and dirty solution. By quickly estimating the crosswind using the above technique, you’ll be able to focus on the task at hand…

Flying on an airplane and learning to navigate successfully.

Landing Limits

Often, airplanes are only certified to land within certain crosswind components. Make an attempt beyond these limits, and you could find yourself in a sticky situation.

How sticky?

Well, aside from potentially losing control of the aircraft, you also risk invalidating any insurance.

Again, when flying an approach, the last thing you want to be doing is having your head in the cockpit crunching numbers. The above ‘clock’ method of making a quick crosswind landing calculation is conservative. It will ensure that you never exceed landing limits, provided you know the wind direction and strength.

Instrument Guidance

Many believe instrument flying (called ‘IFR) is simpler than flying visually.

But…

You may be surprised to learn that you also have to apply wind corrections to instruments too! Maintaining a good instrument scan is hard work at the best of times. To keep that scan rate going, you’ll need a few ‘tricks in the bag’ to estimate crosswind.

The above technique will put you in good stead to achieve this.

Crosswind Landing Technique

There is actually an official technique utilized when landing in a crosswind.

How will you know whether you need to apply it and to what degree unless you can make a valid assessment of the crosswind?

Sure, you may know the crosswind component when you take off, but the wind can change direction completely! By making an ‘on the spot appraisal of the crosswind, you can ensure you apply the right control inputs at the right time.

Wake Turbulence

What would you say if we told you that sometimes a crosswind is a good thing?

While flying smaller airplanes near big airplanes is never a good idea, often the danger might not always be apparent.

Large aircraft leave trails of turbulent air behind them (especially when landing and taking off). This can cause severe upsets to the flight path of a light aircraft.

The good news is that a crosswind can help push this turbulent air away from the runway. How long will you have to wait? Well, that all depends on the crosswind!

Suppose you can make a really quick crosswind assessment while you are waiting to go. In that case, you can be reasonably assured that wake turbulence won’t be a factor!

Final Thoughts…

Performing a quick crosswind calculation is easy once you understand the basic principles. If you can read a watch and understand quarters, you are pretty much good to go. Handy hints like this make learning to fly so much easier. Enjoy this guide? We’ve got plenty more handy ‘hacks’ to help when you are learning to fly. Our online courses make difficult concepts simple and are ideal for new pilots. You can see examples of what we offer here.